Lenses with spherically shaped surfaces. gives rise to several aberrations, for example, spherical aberration due to surface sphericity. One approach to reducing this type of aberration is the use of aspherical surfaces. As shown at the example in Figure below, such lenses feature complex surface shapes, such as paraboloids or even free forms.

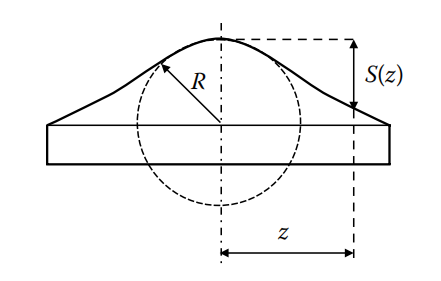
Aspherical surfaces are described by a base sphere with the radius R, a coefficient of asphericity A, and the position-dependent sagitta S(z), according to

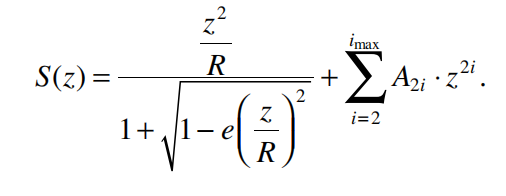
The coordinate z corresponds to half the lens diameter in rotational-symmetric aspheres and is thus equivalent to the ray entrance height of incoming light rays, which propagate parallel to the optical axis of the aspheric lens.

The parameter e in Equation above is referred to as conus constant and defines the geometric basic shape of an aspheric surface as listed in Table below

In addition to spherical and aspherical lenses, cylindrical lenses play an essential role for the realization of high-quality optical systems but also daily-used convenience goods, for example, scanners. Such lenses feature two perpendicular sections on the surface, the meridional and the sagittal. Only one of those sections features a
certain radius of curvature; the other section is represented by a plane. Its radius of curvature is consequently R=0mm. As a result, cylindrical lenses realize focal lines instead of focal points.

If both the meridional and sagittal sections feature different radii of curvature higher than 0mm, the resulting optical component is referred to as a toric lens as shown in Figure below:

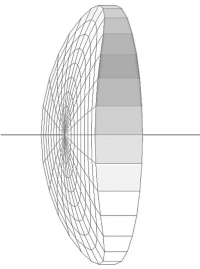
Due to the different radii of curvature of the meridional and sagittal planes, this type of lens produces astigmatism. It is thus a typical lens shape for eye glasses, since astigmatism of the eye lens can be corrected by an appropriate toric surface.