What is spherical lense?
Lenses represent the most important optical components of complex optical systems.
Depending on the geometrical shape or function, lenses can be classified into con verging and diverging ones. Assuming a bundle of light rays propagates parallel to the optical axis of a lens, the first type focuses the light rays into a real focal point 1 due to
refraction at the curved lens surfaces whereas diverging lenses feature a virtual focal point. The particular behavior directly results from the lens shape and the orientation of the curved surfaces. This orientation is expressed by the nominations “convex”
from Latin “convexus”=“curved”) and “*concave*” (from Latin “concavus”=“hollowed”). Usually, a convex lens surface is indicated by the abbreviation “CX” and a concave by “CC” in manufacturing drawings, specifying the basic orientation of curvature. Further, the particular radii of curvature R or Rc, respectively, are given as principally shown at the example of a symmetric biconvex lens in Figure below.
![]()
A complete definition of a lens further requires information about its center thickness tc, its diameter D, and the material (i.e., the glass, in terms of its nominal index of refraction at a predefined reference wavelength, its dispersion characteristics, and material quality regarding acceptable striae, inclusions, birefringence, etc.)
Finally, the surface quality of the optically active surfaces has to
be specified in terms of contour accuracy, cleanliness, surface roughness, etc.,
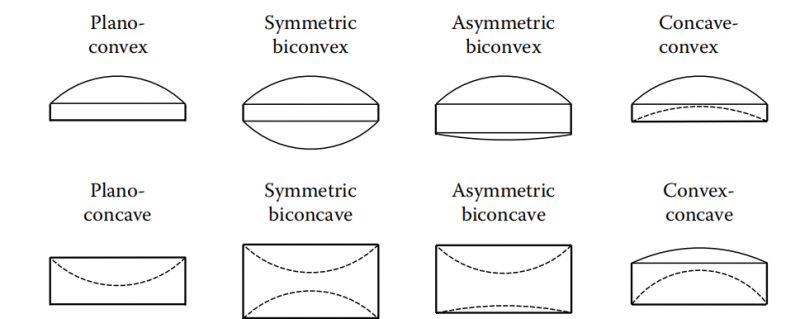
In addition to this mandatory information, related lens parameters such as the sagitta S of a lens surface and the edge thickness te can be derived from the lens geometry via its diameter, radii of curvature, and center thickness. An overview on different lens types and the particular relation between the radii of curvature and the center and edge thickness is given in Table below
| Lens Type | a.k.a | Short Description |
| Converging Lenses | ||
| Plano-convex | R1=∞ and tc > te | |
| Symmetric biconvex | Double convex, convex-concave | R1=R2 and tc > te |
| Asymmetric biconvex | Best form converging lens | R1≠R2 and tc > te |
| Concave-convex | Positive meniscus | Rcc>Rcx and tc > te |
| Diverging Lenses | ||
| Plano-concave a | R1=∞ and tc < te | |
| Symmetric biconcave | Double concave concave-convex | R1=R2 and tc < te |
| Asymmetric biconvex | Best form diverging lens | R1≠R2 and tc < te |
| Concave-convex | Negative meniscus | Rcx>Rcc and tc < te |
It turns out that the center thickness of diverging lenses is smaller than the edge thickness and vice versa, which becomes obvious when looking at the comparison of the above-listed different lens types in Figure below.